Correlation

The correlation is defined as the measure of linear association between two variables. A single value, commonly referred to as the correlation coefficient, is often needed to describe this association.

The value has two special properties. First, most estimates of correlation are bounded by -1 and 1. If the correlation is exactly -1, there is a perfect, negative linear association between the two variables; the scatterplot of the two variables fall along one line with negative slope. Conversely, if the correlation is exactly 1, there is a perfect, positive linear correlation. Secondly, the square of the correlation describes the amount of variability in one variable that is described by the other variable. It should be noted, however, that the correlation coefficient provides no explanation about the physical relationship between the variables.

Caveats / limitations associated with linear correlation:

• Correlation does NOT imply causation or a physical relationship of any kind.
• Correlations are only associated with observed instances of events; further conclusions cannot be inferred from correlations.
• The two datasets must contain similar grids (i.e., independent variables) over which the correlation coefficient is calculated.

*NOTE: The examples below only illustrate correlations over temporal grids. You may correlate over spatial grids by replacing [T] with [X], [Y], [X Y], etc.

The Pearson Product-Moment Correlation

• Pearson product-moment correlation coefficient is the technically correct term for the commonly used term, correlation coefficient.
• Calculated by taking the ratio of the sample covariance of the two variables to the product of the two standard deviations.
  
• Illustrates the strength of linear relationships.
• Coefficient is neither robust nor resistant.
1. Not robust because strong nonlinear relationships between the two variables may not be recognized.
2. Not resistant because it is sensitive to outlying points.

The core of the Pearson correlation coefficient is the covariance between the two variables, or in this case, x and y. Look at the scatterplot below, which illustrates two variables that are positively correlated. The horizontal and vertical lines represent the mean of the data plotted on the y-axis and the x-axis, respectively.


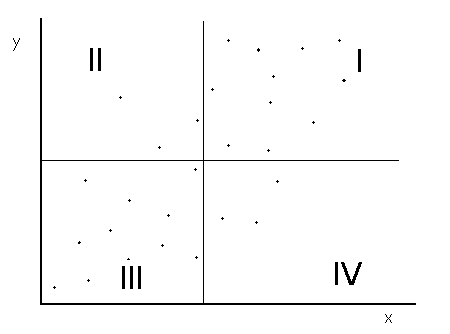
For points in quadrant I, both of the x and y values are larger than their respective means. These points will contribute positive terms to the correlation coefficient. In quadrant III, both the x and y values are less than their respective means, so in the formula for correlation coefficient, the product of the two terms in parenthesis is positive. These points also contribute positive terms to the correlation coefficient. Conversely, points in quadrants II and IV contribute negative terms to the correlation coefficient. Since most of the points fall in quadrants I and III, the correlation coefficient will be dominated by positive terms.


Example: Find the Pearson product-moment correlation between maximum and minimum temperatures at Toyko, Japan for August 1976.

Locate Dataset, Station and Maximum Temperature Variable	Select the "Datasets by Catagory" link in the blue banner on the Data Library page. Click on the "Atmosphere" link. Select the NOAA NCDC GDCN dataset. Click on the "searches" link to the right of the map. In the Name text box under the Searches subheading, enter Tokyo. Click the Search NOAA NCDC GDCN button. Click on the number "47622" which appears below the search text box. CHECK You have selected the station identification number for Tokyo, Japan. Select the "Max Temperature" link under the Datasets and Variables subheading. CHECK
Select Temporal Domain	Click on the "Data Selection" link in the function bar. Enter the text 1 Aug 1976 to 31 Aug 1976 in the Time text box. Press the Restrict Ranges button and then the Stop Selecting button. CHECK
Select Minimum Temperature and Temporal Domain	Click on the "Expert Mode" link in the function bar. Enter the following lines below the text already there: SOURCES .NOAA .NCDC .GDCN ISTA 47662 VALUE .TMIN T (1 Aug 1976) (31 Aug 1976) RANGEEDGES Press the OK button. CHECK
Calculate Pearson Product-Moment Correlation Coefficient	Again in the Expert Mode text box, enter the following line: [T] correlate Press the OK button. CHECK The [T] correlate command computes the Pearson product-moment correlation coefficient for the data over the given range: August 1st-31st, 1976. The result should be located under the Expert Mode text box in bold: 0.8239428. The relatively high correlation coefficient is easily explained. Warm days are usually associated with warm nights and cold days are usually associated with cold nights.

Spearman Rank Correlation

• Data is first sorted and each value assigned a rank, 1 assigned to the lowest value.
• Spearman rank calculated by taking the Pearson product-moment correlation of the ranks of the datasets.
• In cases of ties, where a particular data value appears more than once, all equal values assigned their average rank.
• Robust and resistant alternative to the Pearson product-moment correlation because it is less sensitive to outlying values.
• The rank and product-moment correlations will have dissimilar values due to the different sensitivities of the two methods.

Example: Find the Spearman rank correlation between maximum and minimum temperatures at Toyko, Japan for August 1976.

Locate Dataset, Station and Maximum Temperature Variable	*NOTE: This example uses the same dataset, variable, and ranges as the previous example. Select the "Datasets by Catagory" link in the blue banner on the Data Library page. Click on the "Atmosphere" link. Select the NOAA NCDC GDCN dataset. Click on the "searches" link to the right of the map. In the Name text box under the Searches subheading, enter Tokyo. Click the Search NOAA NCDC GDCN button. Click on the number "47622" which appears below the search text box. CHECK You have selected the station identification number for Tokyo, Japan. Select the "Max Temperature" link under the Datasets and Variables subheading. CHECK
Select Temporal Domain	Click on the "Data Selection" link in the function bar. Enter the text 1 Aug 1976 to 31 Aug 1976 in the Time text box. Press the Restrict Ranges button and then the Stop Selecting button. CHECK
Select Minimum Temperature and Temporal Domain	Click on the "Expert Mode" link in the function bar. Enter the following lines below the text already there: SOURCES .NOAA .NCDC .GDCN ISTA 47662 VALUE .TMIN T (1 Aug 1976) (31 Aug 1976) RANGEEDGES Press the OK button. CHECK
Calculate Spearman Rank Correlation Coefficient	Again in the Expert Mode text box, enter the following line: [T] rankcorrelate Press the OK button. CHECK The [T] rankcorrelate command computes the Spearman correlation coefficient by correlating the ranks of both datasets over the given time range: August 1, 1976 to August 31,1976. The result should be located under the Expert Mode text box in bold: 0.8568417. As in the previous example, there is a relatively high correlation between the two sets of data.

Lagged Correlation

• Lagged correlations found by correlating a lagged dataset with another unlagged dataset using the Pearson product-moment method.
• Lagged data computed by shifting data by a certain unit of time, either forward or backward.
• A positive (negative) lag in time refers to a later (earlier) time. For example, in a data set with a monthly time step, a data point in February 2000 lags the January 2000 data point by a +1 month lag.
• Practical in climatology: often greatest correlation between two variables exhibited using a lagged time step.
• A lag-0 system has no lag applied to it.

Example: Find the lagged correlation between sea surface temperature anomalies and the Southern Oscillation Index from January 1985 to December 2003.

Locate Dataset and Variable	Select the "Datasets by Catagory" link in the blue banner on the Data Library page. Click on the "Air-Sea Interface" link. Scroll down the page and select the NOAA NCEP EMC CMB GLOBAL Reyn_Smith dataset. Click on the "Reyn_SmithOIv2" link. Click on the "monthly" link. Click on the "Sea Surface Temperature Anomaly" link under the Datasets and Variables subheading. CHECK
Select Temporal Domain	Click on the "Data Selection" link in the function bar. Enter the text Jan 1985 to Dec 2003 in the Time text box. Press the Restrict Ranges button and then the Stop Selecting button. CHECK
Add the Standardized SLP Difference SOI Index Dataset with Temporal Domain	Click on the "Expert Mode" link in the function bar. Enter the following line below the text already there: SOURCES .Indices .soi .standardized T (Jan 1985) (Dec 2003) RANGEEDGES Press the OK button. CHECK The above command will enter the SOI dataset into the interface with the same domain as the SSTA dataset.
Compute Lags and Correlate	In the Expert Mode text box, enter the following line below the text already there: T -6 1 6 shiftdatashort Press the OK button. CHECK Here, the shiftdatashort function will shift the SOI data by several lags in time, in effect creating several lagged versions of the data. A new grid will be created with _lag appended to the grid name. In this case 13 lagged versions of the SOI data (from lag -6 to +6 months) will be assigned to the T_lag grid. The monthly time grid "T" will still exist for both the SST and SOI data, but for the SOI data, the time grid will be shortened by six months at each end such that the remaining time grid will include only those time points that are common to all the lagged versions of the SOI data. As mentioned earlier, a positive (negative) lag in time refers to a later (earlier) time. In this case, the lags are all applied to the SOI data. For T_lag = 0, January 2000 SOI data are matched with January 2000 SST data. For T_lag = +1, February 2000 SOI data are matched with January 2000 SST data. So, at T_lag = +1, the February 2000 SOI data are assigned to January 2000 in the time grid. For T_lag = -1, the December 1999 SOI data are assigned to January 2000 (and matched with the January 2000 SST data), and so on for each lag. Complete documentation on the shiftdatashort function is available here. Enter the following command in the Expert Mode text box below the text already there: [T] correlate Press the OK button. CHECK The Pearson product-moment method is used to correlate the sea surface temperature anomalies with the Southern Oscillation Index at each lag interval (i.e. 13 different correlations are calculated).
View Results	To see the results of this operation, choose the viewer window with land shaded in black. CHECK *NOTE: The image may take a few seconds to load. Select different lags by changing the number in the T_lag text box located near the top of the viewer. The image below corresponds to a -6 lag. Pearson Correlation Between SSTA and SOI for -6 Lag Notice the strong negative correlations in the Eastern Pacific. By convention, a negative Southern Oscillation value corresponds to warmer-than-average conditions in the equatorial Pacific while a positive value corresponds to cooler-than-average conditions. Therefore, a negative correlation between SSTA's and SOI values is expected, as shown in the above image.

Autocorrelation

• The correlation between values of the same variable at different times.
• Sometimes referred to as serial correlation.
• Autocorrelation coefficient is calculated by substituting lagged data pairs into the formula for the Pearson product-moment correlation coefficient.
• Autocorrelation function is the collection of autocorrelation coefficients computed for various lags.
1. Function always begins with an autocorrelation coefficient of 1, since a series of unshifted data will exhibit perfect correlation with itself.
2. Function will decay towards zero as lag increases.
• Used to detect non-randomness in data.
• Used to analyze decorrelation time.
1. Indicator of the "memory" or persistence of processes.
2. Dimensionless quantity.
3. Calculated using a positive lag time.
• Used to analyze the effectiveness of persistence forecasts (forecasts consisting of current observations).
1. Persistence forecasts better for processes with long memory than for processes with short memory.
2. Autocorrelation function of a long memory process decays to zero more slowly than that of a short memory process.
3. Calculated using negative lag time.
• Correlation between the persistence forecast and the verifying observation is called the correlation skill score.

Example: Calculate the autocorrelation function and correlation skill score of the NINO 3.4 Index from January 1856 to December 1998.

Locate Dataset and Variable	Select the "Datasets by Catagory" link in the blue banner on the Data Library page. Click on the "Climate Indicies" link. Select the Indicies nino dataset. Select the "EXTENDED" link under the Datasets and Variables subheading. Select the "NINO34" link under the Datasets and Variables subheading. CHECK
Select Temporal Domain	Click on the "Data Selection" link in the function bar. Enter the text Jan 1856 to Dec 1998 in the Time text box. Press the Restrict Ranges button and then the Stop Selecting button. CHECK
Calculate Autocorrelation Function	Click on the "Expert Mode" link in the function bar. Enter the following lines under the text already there: dup T -36 1 1 shiftdatashort [T] correlate Press the OK button. CHECK The dup command duplicates the NINO 3.4 dataset and adds it to the stack. The shiftdatashort command then computes a series of negative lags of the duplicated dataset. This operation results in a series of persistence forecasts of the NINO 3.4 index for each lag. Finally, the correlate command calculates the correlation coefficient between the lagged NINO 3.4 data and the unlagged NINO 3.4 data. *Note that the shiftdatashort function will shorten the range over which the two variables will be correlated. For instance, a -36 lag will correlate values starting at January 1859 because 36 months (3 years) of data were moved foward.
View Autocorrelation Function	To see the results of this operation, choose the time series viewer. In the two text boxes that represent the x-axis ranges, enter 1. and -36. in the left and right boxes, respectively. CHECK This will reverse the order of the lag on the x-axis so that the autocorrelation function is easier to visualize. Autocorrelation Function of the NINO 3.4 Index The autocorrelation function exhibits relatively high values at lags less than 5 months. This is indicative of the "memory" of the NINO 3.4 Index. Persistence forecasts up to a few months may be sufficiently accurate depending on their intended application. Notice that the autocorrelation function crosses zero near -14 months, but then asymptotes back to a correlation of 0 as the lag becomes more negative. Occasionally, the autocorrelation function will oscillate around 0 before eventually decaying to 0.
Find Correlation Skill Score for Individual Lags	Click on the right-most link in the blue source bar to exit the viewer. Select the "Tables" link in the function bar. Click on the "columnar table" link. CHECK Lags smaller than -6 exhibit correlations above 0.5. Also observe that a -1 lag has a correlation of .948. This indicates that a persistance forecast for one month in advance will most likely be quite accurate.

Significance Tables and Correlation

• Used to determine minimum threshold for the correlation coefficient at a given significance level and degree of freedom.
• The 90%, 95%, 98% and 99% two-tailed significance levels of the correlation coefficient are listed in the table below (assuming normally distributed datasets).
• Note that the degrees of freedom (df) = n - 2 for a sample of size n.

df	90%	95%	98%	99%
4	.729	.811	.882	.917
6	.622	.707	.789	.834
8	.549	.632	.716	.765
10	.497	.576	.658	.708
12	.458	.532	.612	.661
14	.426	.497	.574	.623
16	.400	.468	.542	.590
18	.378	.444	.516	.561
20	.360	.423	.492	.537
25	.323	.381	.445	.487
30	.295	.349	.409	.449
35	.275	.325	.381	.418
40	.257	.304	.358	.393
45	.243	.288	.338	.372
50	.231	.273	.322	.354
60	.211	.250	.295	.325
70	.195	.232	.274	.302
80	.183	.217	.256	.283
90	.173	.205	.242	.267
100	.164	.195	.230	.254
200	.116	.138	.164	.181
300	.095	.113	.134	.148
400	.082	.098	.116	.128
500	.073	.088	.104	.115

Example: Find the correlation between average summer (JJA) Sahel rainfall and sea surface temperature anomalies during the time period 1983-1999, and then make a plot of correlation coefficients significant to the 90% level.

Locate Dataset and Variable	Select the "Datasets by Catagory" link in the blue banner on the Data Library page. Click on the "Atmosphere" link. Select the NOAA NCEP CPC CAMS dataset. Select the "mean" link under the Datasets and Variables subheading. Select the "precipitation" link under the Datasets and Variables subheading. CHECK
Select Temporal and Spatial Domains	Click on the "Data Selection" link in the function bar. Enter the text 20W to 40E, 11N to 20N, and Jan 1983 to Dec 1999 in the appropriate text boxes. Press the Restrict Ranges button and then the Stop Selecting button. CHECK
Compute Summer Rainfall Averages	Select the "Expert Mode" link in the function bar. Enter the following lines below the text already there: T 12 splitstreamgrid T (Jul) (Aug) (Sep) VALUES [T]average Press the OK button. CHECK This command splits the time grid into two new time grids. The T grid has a period of 12 months and a step of 1. This grid represents data from January, Februrary, March, etc. The T2 grid has a step of 12 and represents the years from the beginning of the dataset (1999) to the end of the dataset (1999). The following command selects July, August, and September values from the T grid and and the average command averages the rainfall over those three months for each year.
Compute Spatial Average	Click on the "Filters" link in the function bar. Choose Average over "XY" CHECK
Add Reyn_Smith Sea Surface Temperature Anomaly Dataset and Correlate with Precipitation Data	Click on the "Expert Mode" link in the function bar and enter the following lines under the text already there: SOURCES .NOAA .NCEP .EMC .CMB .GLOBAL .Reyn_SmithOIv2 .monthly .ssta T (Jan 1983) (Dec 1999) RANGEEDGES T 12 splitstreamgrid T (Jul) (Aug) (Sep) VALUES [T]average Press the OK button. CHECK The above commands will add the Reyn_Smith monthly SSTA dataset to the interface with the same temporal grid as the CAMS dataset. Again in expert mode, enter the command: [T2] correlate Click the OK button. CHECK This command will correlate the two variables over the time grid T2.
Calculate the 10% Significance Level of the Correlation Coefficient and View Results	Recall that the correlation coefficient was calculated over the years from 1983 to 1999 (a 17-year span) A sample size of 17 results in 15 degrees of freedom using the formula df = n - 2. Find the 90% significance level using the table above. There is no entry for 15 degrees of freedom in the table. Common practice for instances such as this is to use the significance level for the closest number of degrees of freedom BELOW the desired one. This will give a conservative estimate of statistical significance. In this case, you should use the 90% significance level for 14 degrees of freedom, or 0.426. Return to the Expert Mode text box and enter the following lines under the text already there: startcolormap -1 1 RANGEEDGES white black navy -1 value blue -0.8 bandmax DeepSkyBlue -0.6 bandmax aquamarine -0.426 bandmax moccasin dup 0 bandmax moccasin dup 0.426 bandmax yellow DarkOrange 0.6 bandmax red 0.8 bandmax DarkRed 1 bandmax brown endcolormap Press the OK button. CHECK The above colormap commands will create an image with correlation coefficient values between -0.426 and 0.426 masked out. To see the results of this operation, choose the viewer window with land shaded in black. CHECK Correlation Between Summer Sahel Rainfall and SSTA at a 90% Significance Level Note the negative correlations in the Eastern Pacific. These results suggest that during El Niño conditions, when SST's are above normal in the Eastern Pacific, below average summer rainfall in the Sahel is generally observed.